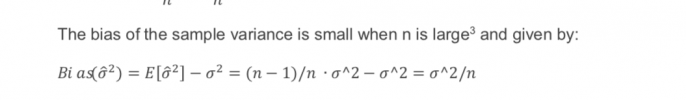You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Bias of the variance
- Thread starter librosdeholanda
- Start date
Hi @librosdeholanda You make a good point, strictly speaking the bias of the sample variance is negative:
(n-1)/n*σ^2 - σ^2
=(n-1)/n*σ^2 - σ^2*n/n
= σ^2*[(n-1)-n]/n
= σ^2*(-1)/n = -σ^2/n
... although we barely need the math: intuitively, the biased (MLE) variance divides by n, while the unbiased variance divides by (n-1) such that the biased variance necessarily smaller than the unbiased variance. I think that because it's bias, we're not overly concerned by the direction of the bias, looks to me like the explanation. Nevertheless, I have to agree with you that strictly it should be negative. Thanks,
(n-1)/n*σ^2 - σ^2
=(n-1)/n*σ^2 - σ^2*n/n
= σ^2*[(n-1)-n]/n
= σ^2*(-1)/n = -σ^2/n
... although we barely need the math: intuitively, the biased (MLE) variance divides by n, while the unbiased variance divides by (n-1) such that the biased variance necessarily smaller than the unbiased variance. I think that because it's bias, we're not overly concerned by the direction of the bias, looks to me like the explanation. Nevertheless, I have to agree with you that strictly it should be negative. Thanks,
Similar threads
- Replies
- 0
- Views
- 721
- Replies
- 2
- Views
- 786
- Replies
- 0
- Views
- 677
- Replies
- 0
- Views
- 572