Hi,
I have the following understanding - Does this make sense or am I missing something here?
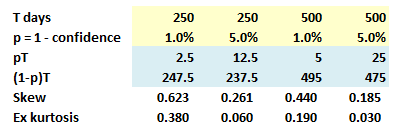
We may choose to accept a 99% VAR model with 95% or 99% (or any other) level of confidence. Hence, using Jorian's example from book, assuming we use a 99% VAR (i.e. p=.01), over 250 days (i.e. T=250). Expected value of exceptions = pT = 2.5. Assume we encountered 8 exceptions. Using Binomial, and as mentioned in the video tutorial by David, the probability of (x=8) will only be 0.3% and cummulative probability of x>8 is only 0.4%. Hence, we can reject this model with 99.6% confidence.
However, on the same example, using normal approximation to binomial (I know we shouldn't use it coz T is only 250 here, and pT = 2.5 which is much lesser than 10, but just for understanding sake).
calculated z score = x-pt/root(p(1-p)T) = 2.23. This is greater than 2 tailed critical z value of 1.96 (for 95% confidence) but smaller than 2 tailed critical z value of 2.6 (for 99% confidence). So, we reject the model at 95% confidence, but we cannot reject with 99% confidence.
Is this correct?
Note: I haven't yet attempted practice questions - so in case the answer is already there, please pardon.
I have the following understanding - Does this make sense or am I missing something here?
We may choose to accept a 99% VAR model with 95% or 99% (or any other) level of confidence. Hence, using Jorian's example from book, assuming we use a 99% VAR (i.e. p=.01), over 250 days (i.e. T=250). Expected value of exceptions = pT = 2.5. Assume we encountered 8 exceptions. Using Binomial, and as mentioned in the video tutorial by David, the probability of (x=8) will only be 0.3% and cummulative probability of x>8 is only 0.4%. Hence, we can reject this model with 99.6% confidence.
However, on the same example, using normal approximation to binomial (I know we shouldn't use it coz T is only 250 here, and pT = 2.5 which is much lesser than 10, but just for understanding sake).
calculated z score = x-pt/root(p(1-p)T) = 2.23. This is greater than 2 tailed critical z value of 1.96 (for 95% confidence) but smaller than 2 tailed critical z value of 2.6 (for 99% confidence). So, we reject the model at 95% confidence, but we cannot reject with 99% confidence.
Is this correct?
Note: I haven't yet attempted practice questions - so in case the answer is already there, please pardon.