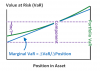
David's ProTip: The Portfolio VaR concepts (marginal, component, incremental, portfolio) are a cluster of related views. Please see that attached diagram, which I reproduced from Jorion. If you can comprehend this single image, you can grasp the concepts qualitatively. The baseline is the green non-linear line: this green line is the plot of portfolio VaR (y axis) against the size of a position. The slope of this line (at a point) is marginal VaR (1st derivative!). Component VaR is the vertical drop, if we remove the position, but according to the (inaccurate) line; incremental VaR is the same but accurately, according to the true non-linear relationship.
AIMs: Describe the challenges associated with VaR measurement as portfolio size increases. Demonstrate how one can use marginal VaR to guide decisions about portfolio VaR. Explain the difference between risk management and portfolio management, and demonstrate how to use marginal VaR in portfolio management
Questions:
3.1. A bank is proposing to add Position (A) to Portfolio (P). (A) is small relative to the large but simple portfolio (P) which is accurately summarized by risk factors that are jointly normally distributed. The bank's Risk Manager seeks a fast and efficient method. Which is the best methods given the situation and the risk manager's preference?
a. Parametric VaR with marginal VaR
b. Full revaluation with incremental VaR
c. Historical Simulation
d. Monte Carlo Simulation
3.2. A bank is proposing to add Position (A) to Portfolio (P). (A) is large relative to (P) and both contain heavy-tailed (i.e., non-normal risk factors) returns that defy distributional assumptions. The bank's Risk Manager needs a method that is computationally simple and easy to communicate. Which is the best methods given the situation and the risk manager's preference?
a. Parametric VaR with marginal VaR
b. Delta-normal VaR
c. Historical Simulation
d. Monte Carlo Simulation
3.3. A bank is proposing to add Position (A) to Portfolio (P). (A) is large relative to portfolio (P) and both are complex with non-normal, non-linear and time-varying exposures. The bank's Risk Manager has a large budget, sophisticated audience and ample computational time such that the priority is precision in the VaR estimate. Which is the best methods given the situation and the risk manager's preference?
a. Parametric VaR with marginal VaR
b. Delta-normal VaR
c. Historical Simulation
d. Monte Carlo Simulation
3.4. If the goal is to shift a portfolio to its global risk minimum (global minimum-risk), per the perspective of a risk manager, which of the following is most effective?
a. Add (trim) positions with low (high) Sharpe ratios until Sharpe ratios are equal
b. Add (trim) positions with low (high) marginal VaR until Marginal VaRs are equal
c. Add (trim) positions with low (high) ratios of excess return to beta until ratios (excess return/beta) are equal
d. Add (trim) positions with low (high) ratios of Individual VaR to Portfolio VaR until ratios (Individual VaR/Portfolio VaR) are equal
3.5. If the goal is to shift a portfolio to the optimal portfolio, per the reward/risk perspective of a portfolio manager, which of the following is most effective?
a. Add (trim) positions with low (high) Sharpe ratios until Sharpe ratios are equal
b. Add (trim) positions with low (high) marginal VaR until Marginal VaRs are equal
c. Add (trim) positions with low (high) ratios of excess return to beta until ratios (excess return/beta) are equal
d. Add (trim) positions with low (high) ratios of Individual VaR to Portfolio VaR until ratios (Individual VaR/Portfolio VaR) are equal
Answers:
AIMs: Describe the challenges associated with VaR measurement as portfolio size increases. Demonstrate how one can use marginal VaR to guide decisions about portfolio VaR. Explain the difference between risk management and portfolio management, and demonstrate how to use marginal VaR in portfolio management
Questions:
3.1. A bank is proposing to add Position (A) to Portfolio (P). (A) is small relative to the large but simple portfolio (P) which is accurately summarized by risk factors that are jointly normally distributed. The bank's Risk Manager seeks a fast and efficient method. Which is the best methods given the situation and the risk manager's preference?
a. Parametric VaR with marginal VaR
b. Full revaluation with incremental VaR
c. Historical Simulation
d. Monte Carlo Simulation
3.2. A bank is proposing to add Position (A) to Portfolio (P). (A) is large relative to (P) and both contain heavy-tailed (i.e., non-normal risk factors) returns that defy distributional assumptions. The bank's Risk Manager needs a method that is computationally simple and easy to communicate. Which is the best methods given the situation and the risk manager's preference?
a. Parametric VaR with marginal VaR
b. Delta-normal VaR
c. Historical Simulation
d. Monte Carlo Simulation
3.3. A bank is proposing to add Position (A) to Portfolio (P). (A) is large relative to portfolio (P) and both are complex with non-normal, non-linear and time-varying exposures. The bank's Risk Manager has a large budget, sophisticated audience and ample computational time such that the priority is precision in the VaR estimate. Which is the best methods given the situation and the risk manager's preference?
a. Parametric VaR with marginal VaR
b. Delta-normal VaR
c. Historical Simulation
d. Monte Carlo Simulation
3.4. If the goal is to shift a portfolio to its global risk minimum (global minimum-risk), per the perspective of a risk manager, which of the following is most effective?
a. Add (trim) positions with low (high) Sharpe ratios until Sharpe ratios are equal
b. Add (trim) positions with low (high) marginal VaR until Marginal VaRs are equal
c. Add (trim) positions with low (high) ratios of excess return to beta until ratios (excess return/beta) are equal
d. Add (trim) positions with low (high) ratios of Individual VaR to Portfolio VaR until ratios (Individual VaR/Portfolio VaR) are equal
3.5. If the goal is to shift a portfolio to the optimal portfolio, per the reward/risk perspective of a portfolio manager, which of the following is most effective?
a. Add (trim) positions with low (high) Sharpe ratios until Sharpe ratios are equal
b. Add (trim) positions with low (high) marginal VaR until Marginal VaRs are equal
c. Add (trim) positions with low (high) ratios of excess return to beta until ratios (excess return/beta) are equal
d. Add (trim) positions with low (high) ratios of Individual VaR to Portfolio VaR until ratios (Individual VaR/Portfolio VaR) are equal
Answers: