Level I (Questions 1-20) FRM 2010 Practice Questions – Vol. I
- Thread starter skoh
- Start date
Also could you kindly explain on how to derive the answer for question 17? I was looking through the z-table but I don't understand how to get 0.0228 for 82.5?
Assume that a random variable follows a normal distribution with a mean of 100 and a standard deviation of 17.5.What is the probability that this random variable is between 82.5 and 135?
a) 68.0%
b) 81.9%
c) 82.8%
d) 95.0%
Answer:
Prob (-1*σ < X < 2*σ) = (1 - 0.0228) - 0.1587 = 0.8185
82.5 = 100 - 17.5 and 135 = 100 + 2 * 17.5. So, the percentage is 34% on the left hand side of the mean, plus 95%/2 on the right hand side of the mean.
Assume that a random variable follows a normal distribution with a mean of 100 and a standard deviation of 17.5.What is the probability that this random variable is between 82.5 and 135?
a) 68.0%
b) 81.9%
c) 82.8%
d) 95.0%
Answer:
Prob (-1*σ < X < 2*σ) = (1 - 0.0228) - 0.1587 = 0.8185
82.5 = 100 - 17.5 and 135 = 100 + 2 * 17.5. So, the percentage is 34% on the left hand side of the mean, plus 95%/2 on the right hand side of the mean.
Hi skoh,
1. No, the 2*Δy is used when the prices in the numerator are shocked by +/- Δy. The difference between Price at (y0+Δy) and Price at (y0-Δy) is a price difference due to 2*Δy. This is a totally understandable mistake and why it's helpful to understand that effective duration = slope * -1/P; i.e., it's just a rise/run where you want the price difference (rise) to match the yield difference (run), please see: http://forum.bionicturtle.com/threa...uration-and-general-question.6846/#post-23455
2. I'm not sure why they used (1-0.0228) but it goes to show how we want to be comfortable with normal symmetry. If we want the probability at -2 standard deviations (i.e., 82.5), a lookup table in a stat book might only give us positive Zs (the right-hand side of the standard normal). So we would need to find Pr[Z < 2.0] = 0.9772, see below. That tells us that 97.72% of the standard normal is left of +2.0 Z. We want all of that probability except for the left tail where X < 1 sigma = Pr[Z < -1] = 1 - Pr[Z < +1] = 1 - 0.8413 = 15.87%
i.e., we need to be able to use Pr[Z < +1.0] in the lookup table in order to deduce Pr[Z < -1.0] per symmetry.
so Pr[ -1 < Z < +2] = 97.72% is all area left of +2 minus (-) 15.87% is area left of -1.0 = 81.86%
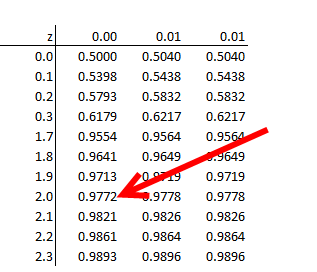
I hope that helps,
1. No, the 2*Δy is used when the prices in the numerator are shocked by +/- Δy. The difference between Price at (y0+Δy) and Price at (y0-Δy) is a price difference due to 2*Δy. This is a totally understandable mistake and why it's helpful to understand that effective duration = slope * -1/P; i.e., it's just a rise/run where you want the price difference (rise) to match the yield difference (run), please see: http://forum.bionicturtle.com/threa...uration-and-general-question.6846/#post-23455
2. I'm not sure why they used (1-0.0228) but it goes to show how we want to be comfortable with normal symmetry. If we want the probability at -2 standard deviations (i.e., 82.5), a lookup table in a stat book might only give us positive Zs (the right-hand side of the standard normal). So we would need to find Pr[Z < 2.0] = 0.9772, see below. That tells us that 97.72% of the standard normal is left of +2.0 Z. We want all of that probability except for the left tail where X < 1 sigma = Pr[Z < -1] = 1 - Pr[Z < +1] = 1 - 0.8413 = 15.87%
i.e., we need to be able to use Pr[Z < +1.0] in the lookup table in order to deduce Pr[Z < -1.0] per symmetry.
so Pr[ -1 < Z < +2] = 97.72% is all area left of +2 minus (-) 15.87% is area left of -1.0 = 81.86%
I hope that helps,
Similar threads
- Sticky
