Learning objectives: Explain the role of linear regression and logistic regression in prediction. Understand how to encode categorical variables.
Questions:
23.6.1. Darlene is a risk analyst who evaluates the creditworthiness of loan applicants at her financial institution. Her department is testing a new logistic regression model. If the model performs well in testing, it will be deployed to assist in the underwriting decision-making process. The training data is a sub-sample (n = 800) from the same LendingClub database used in reading. In the logistic regression, the dependent variable is a 0/1 for the terminal state of the loan being either zero (fully paid off) or one (deemed irrecoverable or defaulted). In the actual code, this dependent variable is labeled 'outcome'.
The following are the features (aka, independent variables) as given by their textual labels: Amount, Term, Interest_rate, Installment, Employ_hist, Income, and Bankruptcies. In regard to units in the database, please note the following: Amount is thousands of dollars ($000s); Term is months; Interest_rate is effectively multiplied by one hundred such that 7 equates to 7% or 0.070; Installment is dollars; Employment_hist is years; Income is thousand of dollars ($000); and Bankruptcies is a whole number {0, 1, 2, ...}.
The table below displays the logistic regression results:
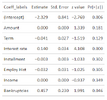
In regard to this logistic regression, each of the following statements is true EXCEPT which is false?
a. A single additional bankruptcy increases the expected odds of default by almost 58 percent
b. If she requires significance at the 5% level or better, then two of the coefficients (in addition to the intercept) are significant
c. Each +100 basis points increase in the interest rate (e.g., from 8.0% to 9.0%) implies an increase of about 14.0 basis points in the default probability
d. If the cost of making a bad loan is high, she can decrease the threshold (i.e., set Z to a low value such as 0.05), but this will reject more good borrowers
23.6.2. Donald wants to fit a logistic regression model in order to predict whether an individual will incur any late fees in their first year of credit card usage; i.e., the dependent response is a Bernoulli-distributed variable. Specifically, zero (0) will signify the borrower makes all payments on time; one (1) will signify at least one delinquency. The databases contain a categorical field (aka, feature) called Employ_status, and all observations in the training set contain one of the following five values to capture the applicant's primary employment status: {unemployed, employed, homemaker, student, retired}.
Which of the following is Donald's best approach to handling the Employ_status feature?
a. He should create four dummy variables
b. He should create five dummy variables
c. He should avoid dummy variables and retain a single independent variable (Employ_status) that contains integer values {1, 2, 3, 4, 5}
d. He should exclude this feature for the logistic regression; or if he wants to retain the feature, he should switch to linear regression
23.6.3. Carla fits a logistic regression model to her training data that predicts whether a corporate credit facility will default. Binary coding informs the response (aka, dependent) variable such that y(i) = zero (0) to signify repayment and y(i) = one (1) to signify default or nonpayment. Her model has three predictors (aka, independent variables) as follows:
α = -3.00, β1 = -0.40, β2 = 1.50, and β3 = 0.70.
As a logistic regression, the probability of default is given by P(X) = 1/[1 +exp(-y)] where y = α + β1*X1 + β2*X2 + β3*X3.
Which of the following statements is true?
a. There must be a mistake in the model because the intercept cannot be negative in logistic regression
b. A one-unit increase in the client's leverage (e.g., 0.20 to 1.20) implies the predicted odds of default will roughly double
c. For a client with an internal credit rating of 5, leverage of 2.0, and zero delinquencies, the model predicts a default probability of 10.90%
d. A one-unit increase in the client's internal credit rating (e.g., from 5 to 6) implies the predicted default probability will drop by about 40 basis points
Answers:
Questions:
23.6.1. Darlene is a risk analyst who evaluates the creditworthiness of loan applicants at her financial institution. Her department is testing a new logistic regression model. If the model performs well in testing, it will be deployed to assist in the underwriting decision-making process. The training data is a sub-sample (n = 800) from the same LendingClub database used in reading. In the logistic regression, the dependent variable is a 0/1 for the terminal state of the loan being either zero (fully paid off) or one (deemed irrecoverable or defaulted). In the actual code, this dependent variable is labeled 'outcome'.
The following are the features (aka, independent variables) as given by their textual labels: Amount, Term, Interest_rate, Installment, Employ_hist, Income, and Bankruptcies. In regard to units in the database, please note the following: Amount is thousands of dollars ($000s); Term is months; Interest_rate is effectively multiplied by one hundred such that 7 equates to 7% or 0.070; Installment is dollars; Employment_hist is years; Income is thousand of dollars ($000); and Bankruptcies is a whole number {0, 1, 2, ...}.
The table below displays the logistic regression results:

In regard to this logistic regression, each of the following statements is true EXCEPT which is false?
a. A single additional bankruptcy increases the expected odds of default by almost 58 percent
b. If she requires significance at the 5% level or better, then two of the coefficients (in addition to the intercept) are significant
c. Each +100 basis points increase in the interest rate (e.g., from 8.0% to 9.0%) implies an increase of about 14.0 basis points in the default probability
d. If the cost of making a bad loan is high, she can decrease the threshold (i.e., set Z to a low value such as 0.05), but this will reject more good borrowers
23.6.2. Donald wants to fit a logistic regression model in order to predict whether an individual will incur any late fees in their first year of credit card usage; i.e., the dependent response is a Bernoulli-distributed variable. Specifically, zero (0) will signify the borrower makes all payments on time; one (1) will signify at least one delinquency. The databases contain a categorical field (aka, feature) called Employ_status, and all observations in the training set contain one of the following five values to capture the applicant's primary employment status: {unemployed, employed, homemaker, student, retired}.
Which of the following is Donald's best approach to handling the Employ_status feature?
a. He should create four dummy variables
b. He should create five dummy variables
c. He should avoid dummy variables and retain a single independent variable (Employ_status) that contains integer values {1, 2, 3, 4, 5}
d. He should exclude this feature for the logistic regression; or if he wants to retain the feature, he should switch to linear regression
23.6.3. Carla fits a logistic regression model to her training data that predicts whether a corporate credit facility will default. Binary coding informs the response (aka, dependent) variable such that y(i) = zero (0) to signify repayment and y(i) = one (1) to signify default or nonpayment. Her model has three predictors (aka, independent variables) as follows:
- X1 is her bank's internal credit rating: an integer from 1 to 10, where 10 is the highest credit quality
- X2 is the number of late payments (or delinquencies) by the client. Most have zero, but several have one or even two or three.
- X3 is the client's balance sheet leverage after the credit facility, as measured by the total debt-to-equity ratio. For example, 0.20 is low leverage, but many prospects have a leverage that greatly exceeds one.
α = -3.00, β1 = -0.40, β2 = 1.50, and β3 = 0.70.
As a logistic regression, the probability of default is given by P(X) = 1/[1 +exp(-y)] where y = α + β1*X1 + β2*X2 + β3*X3.
Which of the following statements is true?
a. There must be a mistake in the model because the intercept cannot be negative in logistic regression
b. A one-unit increase in the client's leverage (e.g., 0.20 to 1.20) implies the predicted odds of default will roughly double
c. For a client with an internal credit rating of 5, leverage of 2.0, and zero delinquencies, the model predicts a default probability of 10.90%
d. A one-unit increase in the client's internal credit rating (e.g., from 5 to 6) implies the predicted default probability will drop by about 40 basis points
Answers:
Last edited by a moderator:
