P1.T4.813. Binomial model for options on currencies and futures (Hull Ch.13)

[Nicole Seaman]

Learning objectives: Explain how the binomial model can be altered to price options on: ... currencies, and futures. Define and calculate delta of a stock option.

Questions:

813.1. Below is illustrated the two-step binomial tree implied by the following assumptions for a six-month put option: S(0) = $75.00, K = $70.00, volatility (σ) = 25.0% per annum, risk-free rate = 4.0%. The two-step model (i.e., Δt 0.50 years/2 = 0.25) returns an price of $2.74 for this out-of-the-money put:

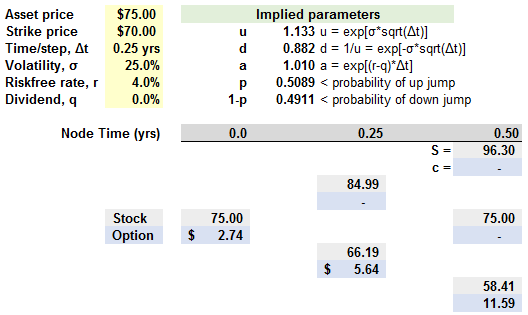
Which of the following are nearest to, respectively, the option's delta (i) over the first time step, and (ii) over the second time step if there is a downward movement in the first step? note: this is equivalent to asking, what is the option's delta at, respectively, node(0,0) and node(1,0)?

a. -0.30 and -0.70
b. -0.50 and -1.00
c. -0.65 and -0.85
d. +0.33 and +0.67


813.2. The Euro is currently worth $1.20 U.S. dollars and this exchange rate (i.e., $1.20 EURUSD) has a volatility of 34.0%. The Euro's risk-free rate is 5.0% and the U.S. risk-free rate is 4.0%. If we use a three-step binomial tree to value an American-style call option with a strike price of $1.00 and a maturity of three months (0.25 years), which is nearest to the value of the option? (based on Hull's Example 13.2)

a. $0.2130
b. $0.3690
c. $0.4077
d. $0.5240


813.3. A futures price is currently $25.00 and has a volatility of 40.0%. The risk-free rate is 3.0%. If we use a three-step tree to value a nine (9) month put option with a strike price of $20.00 on the futures contract, which is nearest to the value of the option? (based on Hull's Example 13.3)

a. $0.54
b. $1.02
c. $3.65
d. $9.87

Answers here:

• In forum

 

[flex]

hi, All. is (Am/European) type of the option should be specified at QSTN 813.1 or answ is an independ from it condition?

 

[David Harper CFA FRM]

Hi @flex in my option, it is not necessary to specify European/American style: in the binomial tree, if it were American with early exercise, this would be reflected in a MAX() as each node such that the delta calculation remains Δc/ΔS. Put simply, because we are given the fully specified tree, the $2.74 value (and other nodes) already reflect early exercise, or lack thereof. Thanks for a good question, it's good to ask such questions I think!