AIMs: Describe volatility term structures and volatility surfaces and how they may be used to price options. Explain the impact of the volatility smile on the calculation of the “Greeks.” Explain the impact of asset price jumps on volatility smiles
Questions:
411.1. The table below illustrates a volatility surface (an exaggeration variation on Hull's Table 19.2). The main body of the table shows implied volatilities calculated from the Black-Scholes-Merton (BSM) model. One dimension of the table is maturity; the other dimension is strike divided by asset price, K/[S(0)]. Implied volatilities are (hypothetically) calculated from traded options; for example, there exists a traded market price for a one-year at-the-money (ATM) option price such that its implied volatility is 22.10%:
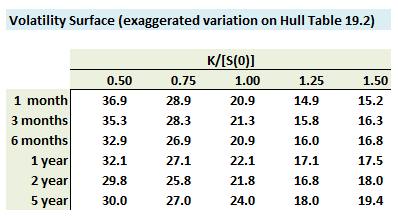
Currently the asset price, S(0), is $30.00. In order to value an out-of-the-money (OTM) call option with a strike price of $33.00 and a maturity of 4.0 years, a trader wants to obtain an implied volatility in order to use the BSM option pricing model. Which is nearest to the implied volatility estimate?
a. 18.76
b. 19.50
c. 21.00
d. 22.33
411.2. Based on the traded market price of $13.28 for a one-year at-the-money (ATM) call option with a strike price of $100.00, Peter the Risk Analyst infers an implied volatility of 30.0% per annum. According to the Black-Scholes-Merton option pricing model, the call option's delta, N(d1), is 0.60 such that the corresponding put option delta (i.e., for a put option with the same $100.00 strike price and one-year maturity) is N(d1)-1.0 = 0.60 - 1.0 = -0.40. However, the equity option exhibits a rather steep implied volatility skew which implies, relative to the lognormal distribution, heavy left tails and light right tails: implied volatility is a decreasing function of the K/[S(0)]. Which of the following describes the relationship between true delta and the deltas (0.60 and -0.40) given exclusively by the BSM pricing model?
a. true call option delta is higher than 0.60 and true put option delta is higher than -0.40
b. true call option delta is lower than 0.60 and true put option delta is lower than -0.40
c. true call option delta is equal to 0.60 and true put option delta is equal to -0.40
d. The relationship is unclear because delta is a linear approximation; it is only the first partial derivative
411.3. Suppose a stock price is currently $50.00 while the risk-free rate is 3.0% per annum. For a series of options with a three month (0.25 years) maturity, the implied volatility is calculated at various strike prices, as below (this is a variation on Hull's Table 19.3):
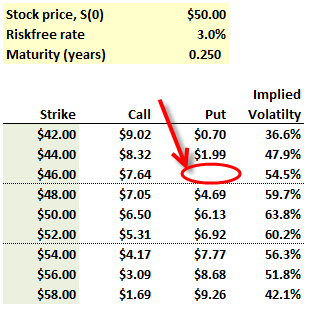
a. The market price (trades) of the put is $3.30 and this is lower than the BSM model-based price which assumes an (ATM) volatility of 63.8%
b. The market price (trades) of the put is $3.30 and this is higher than the BSM model-based price which assumes an (ATM) volatility of 63.8%
c. The market price (trades) of the put is $4.13 and this is lower than the BSM model-based price which assumes an (ATM) volatility of 63.8%
d. The market price (trades) of the put is $4.13 and this is equal to the BSM model-based price which assumes an (ATM) volatility of 63.8%
Answers here:
Questions:
411.1. The table below illustrates a volatility surface (an exaggeration variation on Hull's Table 19.2). The main body of the table shows implied volatilities calculated from the Black-Scholes-Merton (BSM) model. One dimension of the table is maturity; the other dimension is strike divided by asset price, K/[S(0)]. Implied volatilities are (hypothetically) calculated from traded options; for example, there exists a traded market price for a one-year at-the-money (ATM) option price such that its implied volatility is 22.10%:

Currently the asset price, S(0), is $30.00. In order to value an out-of-the-money (OTM) call option with a strike price of $33.00 and a maturity of 4.0 years, a trader wants to obtain an implied volatility in order to use the BSM option pricing model. Which is nearest to the implied volatility estimate?
a. 18.76
b. 19.50
c. 21.00
d. 22.33
411.2. Based on the traded market price of $13.28 for a one-year at-the-money (ATM) call option with a strike price of $100.00, Peter the Risk Analyst infers an implied volatility of 30.0% per annum. According to the Black-Scholes-Merton option pricing model, the call option's delta, N(d1), is 0.60 such that the corresponding put option delta (i.e., for a put option with the same $100.00 strike price and one-year maturity) is N(d1)-1.0 = 0.60 - 1.0 = -0.40. However, the equity option exhibits a rather steep implied volatility skew which implies, relative to the lognormal distribution, heavy left tails and light right tails: implied volatility is a decreasing function of the K/[S(0)]. Which of the following describes the relationship between true delta and the deltas (0.60 and -0.40) given exclusively by the BSM pricing model?
a. true call option delta is higher than 0.60 and true put option delta is higher than -0.40
b. true call option delta is lower than 0.60 and true put option delta is lower than -0.40
c. true call option delta is equal to 0.60 and true put option delta is equal to -0.40
d. The relationship is unclear because delta is a linear approximation; it is only the first partial derivative
411.3. Suppose a stock price is currently $50.00 while the risk-free rate is 3.0% per annum. For a series of options with a three month (0.25 years) maturity, the implied volatility is calculated at various strike prices, as below (this is a variation on Hull's Table 19.3):

a. The market price (trades) of the put is $3.30 and this is lower than the BSM model-based price which assumes an (ATM) volatility of 63.8%
b. The market price (trades) of the put is $3.30 and this is higher than the BSM model-based price which assumes an (ATM) volatility of 63.8%
c. The market price (trades) of the put is $4.13 and this is lower than the BSM model-based price which assumes an (ATM) volatility of 63.8%
d. The market price (trades) of the put is $4.13 and this is equal to the BSM model-based price which assumes an (ATM) volatility of 63.8%
Answers here:
