Learning outcome: Describe financial correlation risk and the areas in which it appears in finance.
Questions:
501.1. Below are displayed seven pairs of (A,B) variables; e.g., (3,5), (4,4)...(7,1). The third row shows pairwise products; e.g., 3*5 = 15, 4*4 = 16. Finally, the mean, E(.), and standard deviation, StdDev(.), are displayed; e.g., E(A) = 5.860, E(A*B) = 17.710, Standard Deviation (A*B) = 6.250. Note the StdDev(.) is a population's standard deviation; we do not require the sample standard deviations (why?).
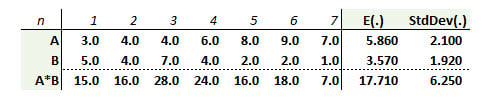
Which is nearest to the Pearson correlation coefficient between (A) and (B)?
a. -0.80
b. -0.33
c. +0.07
d. +0.24
501.2. A popular group of correlation options are multi-asset options; aka, rainbow options or mountain range options. In the choices below, S1 is the price of asset #1 and S2 is the price of asset #2 at option maturity. K is the strike price, i.e., the price determined at option start, at which the underlying asset can be bought in the case of a call, and the price at which the underlying asset can be sold in the case of a put. For which of the following multi-asset options does an an increase in correlation between the asset prices S1 and S2 imply an increase in the option price?
a. Call on the maximum of two: Payoff = max[0, max(S1, S2) - K]
b. Option on the worse of two: Payoff = min(S1, S2)
c. Exchange option: Payoff = max (0, S2 - S1)
d. Spread call option: Payoff = max[0, (S2 - S1) - K]
501.3. Commercial bank (C) has lent to company (A) and company (B). Both (A) and (B) have a 9.0% default probability. If their pairwise default correlation is 0.280, which is nearest to the joint probability of default (we can use the referenced binomial correlation measure of Lucas 1995, but it is available to us with application of FRM Part 1 concepts)?
a. 0.81%
b. 3.10%
c. 6.20%
d. 8.72%
Answers here:
Questions:
501.1. Below are displayed seven pairs of (A,B) variables; e.g., (3,5), (4,4)...(7,1). The third row shows pairwise products; e.g., 3*5 = 15, 4*4 = 16. Finally, the mean, E(.), and standard deviation, StdDev(.), are displayed; e.g., E(A) = 5.860, E(A*B) = 17.710, Standard Deviation (A*B) = 6.250. Note the StdDev(.) is a population's standard deviation; we do not require the sample standard deviations (why?).

Which is nearest to the Pearson correlation coefficient between (A) and (B)?
a. -0.80
b. -0.33
c. +0.07
d. +0.24
501.2. A popular group of correlation options are multi-asset options; aka, rainbow options or mountain range options. In the choices below, S1 is the price of asset #1 and S2 is the price of asset #2 at option maturity. K is the strike price, i.e., the price determined at option start, at which the underlying asset can be bought in the case of a call, and the price at which the underlying asset can be sold in the case of a put. For which of the following multi-asset options does an an increase in correlation between the asset prices S1 and S2 imply an increase in the option price?
a. Call on the maximum of two: Payoff = max[0, max(S1, S2) - K]
b. Option on the worse of two: Payoff = min(S1, S2)
c. Exchange option: Payoff = max (0, S2 - S1)
d. Spread call option: Payoff = max[0, (S2 - S1) - K]
501.3. Commercial bank (C) has lent to company (A) and company (B). Both (A) and (B) have a 9.0% default probability. If their pairwise default correlation is 0.280, which is nearest to the joint probability of default (we can use the referenced binomial correlation measure of Lucas 1995, but it is available to us with application of FRM Part 1 concepts)?
a. 0.81%
b. 3.10%
c. 6.20%
d. 8.72%
Answers here:
