Learning objectives: Explain how payment frequencies and exercise dates affect the exposure profile of various securities. Explain the impact of netting on exposure, the benefit of correlation, and calculate the netting factor.
Questions:
911.1. Consider the following exposure profile for a five-year credit default swap (CDS):
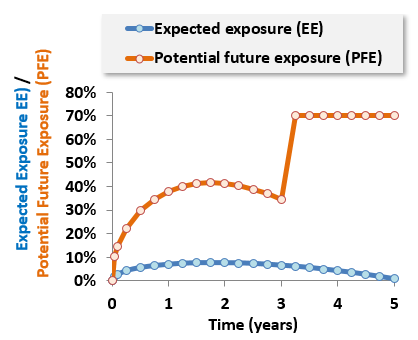
Given this profile, which of the following statements is TRUE?
a. The key parameter that informs the shape of the expected exposure profile is the recovery rate
b. The expected exposure (EE) profile is incorrectly graphed because its shape should resemble the PFE; that is, it should also contain an abrupt jump
c. At year three and beyond, the simulated default probability begins to exceed one minus the potential future exposure (PFE) confidence level; i.e., PD(3+ years) > α = (1 - C)
d. If we wanted to artificially force the PFE curve to match (ie, overlap) the EE curve, we could keep lowering the interest rate parameter until the PFE falls to meet the EE curve
911.2. Gregory defines the netting factor as the ratio of net to gross exposure such that a netting factor of 100.0% represents no benefit while a netting factor of 0% represents maximum netting benefit. (Source: Jon Gregory, The xVA Challenge: Counterparty Credit Risk, Funding, Collateral, and Capital, 3rd edition (West Sussex, UK: John Wiley & Sons, 2015))
Assume there are eight independent transactions with equal volatility; i.e., n = 8, average correlation ρ = 0, and σ(i) = same. What is the implied netting factor?
a. 12.5%
b. 35.4%
c. 75.0%
d. 87.5%
911.3. Consider two trades under the five scenarios illustrated below:
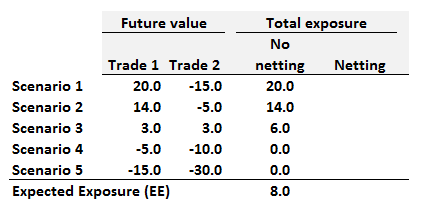
What is the netting factor?
a. 12.5%
b. 25.0%
c. 50.0%
d. 75.0%
Answers here:
Questions:
911.1. Consider the following exposure profile for a five-year credit default swap (CDS):

Given this profile, which of the following statements is TRUE?
a. The key parameter that informs the shape of the expected exposure profile is the recovery rate
b. The expected exposure (EE) profile is incorrectly graphed because its shape should resemble the PFE; that is, it should also contain an abrupt jump
c. At year three and beyond, the simulated default probability begins to exceed one minus the potential future exposure (PFE) confidence level; i.e., PD(3+ years) > α = (1 - C)
d. If we wanted to artificially force the PFE curve to match (ie, overlap) the EE curve, we could keep lowering the interest rate parameter until the PFE falls to meet the EE curve
911.2. Gregory defines the netting factor as the ratio of net to gross exposure such that a netting factor of 100.0% represents no benefit while a netting factor of 0% represents maximum netting benefit. (Source: Jon Gregory, The xVA Challenge: Counterparty Credit Risk, Funding, Collateral, and Capital, 3rd edition (West Sussex, UK: John Wiley & Sons, 2015))
Assume there are eight independent transactions with equal volatility; i.e., n = 8, average correlation ρ = 0, and σ(i) = same. What is the implied netting factor?
a. 12.5%
b. 35.4%
c. 75.0%
d. 87.5%
911.3. Consider two trades under the five scenarios illustrated below:

What is the netting factor?
a. 12.5%
b. 25.0%
c. 50.0%
d. 75.0%
Answers here:
