Learning objectives: Evaluate the characteristics of illiquid markets. Examine the relationship between market imperfections and illiquidity. Assess the impact of biases on reported returns for illiquid assets. Describe the unsmoothing of returns and its properties.
Questions:
707.1. According to Andrew Ang, illiquidity can arise due to the following market imperfections: Clientèle effects and participation costs, transaction costs, search frictions, asymmetric information, price impact or funding constraints. He characterizes the effects of these imperfections as "illiquidity." In regard to the CHARACTERISTICS of illiquid markets, based on Ang's research, which of the following statements is TRUE (such that the other statements are generally false)?
a. Normally liquid markets periodically become illiquid
b. Most individuals hold the majority of their wealth in liquid or highly liquid assets
c. Most asset classes are liquid such that genuinely illiquid markets tend to be small and temporary
d. Technology has virtually eliminated the following frictions: transaction costs, search friction, asymmetric information, price impact, and funding constraints
707.2. Andrew Ang makes an important, provocative statement when he writes "Reported illiquid asset returns are not returns." He claims that people overstate the expected returns and understate the risk of illiquid assets, and he attributes this to three key biases. According to Ang, each of the following is a bias that overstates the expected returns (and/or understates the risk) of illiquid assets EXCEPT which is not accurate?
a. Survivorship bias can inflate returns by 4.0% or more
b. Infrequent sampling (aka, infrequent trading) artificially reduces risk and risk-related metrics such as volatility, correlation and beta
c. Turnover bias decreases the typical time between transactions and tends to artificially increase the expected return by 5.0% or more
d. Selection bias (aka, reporting bias) is a distortion of the sample that artificially increases (ie, overestimates) alpha and artificially decreases (ie, underestimates) beta
707.3. To adjust the infrequent trading bias introduced that is introduced into reported returns, we can "unsmooth" or "de-smooth" the reported returns. Ang suggests this is a filtering problem: "Filtering algorithms are normally used to separate signals from noise. When we’re driving on a freeway and talking on a cell phone, our phone call encounters interference—from highway overpasses and tall buildings—or the reception becomes patchy when we pass through an area without enough cell phone towers. Telecommunication engineers use clever algorithms to enhance the signal, which carries our voice, against all the static. The full transmission contains both the signal and noise, and so the true signal is less volatile than the full transmission. Thus standard filtering problems are designed to remove noise. The key difference is that unsmoothing adds noise back to the reported returns to uncover the true returns."
The essence of unsmoothing of returns is illustrated by Ang's formulas 13.1, 13.2 and 13.4 below:
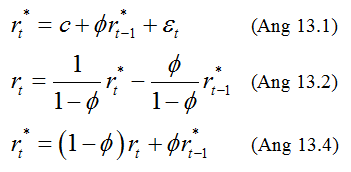
In these formulas r*(t) is the reported (aka, observed) return and r(t) is the true but unobserved return. Importantly, as is almost always the case in finance, the model used in this particular unsmoothing process makes key assumptions. However, if the assumptions are correct, then each of the following statements about the unsmoothing process is true EXCEPT which is false?
a. Unsmoothing affects only risk estimates and not expected returns
b. Unsmoothing has no effect if the observed returns are uncorrelated.
c. The true returns implied by the "transfer function" and equation 13.2, r(t), should have zero autocorrelation and generally should not be themselves forecastable
d. Due to the autocorrelation assumption, |φ| <1, the variance of the true returns will be less than the variance of the observed returns; i.e., variance[r(t)] < i.e., variance[r*(t)]
Answers here:
Questions:
707.1. According to Andrew Ang, illiquidity can arise due to the following market imperfections: Clientèle effects and participation costs, transaction costs, search frictions, asymmetric information, price impact or funding constraints. He characterizes the effects of these imperfections as "illiquidity." In regard to the CHARACTERISTICS of illiquid markets, based on Ang's research, which of the following statements is TRUE (such that the other statements are generally false)?
a. Normally liquid markets periodically become illiquid
b. Most individuals hold the majority of their wealth in liquid or highly liquid assets
c. Most asset classes are liquid such that genuinely illiquid markets tend to be small and temporary
d. Technology has virtually eliminated the following frictions: transaction costs, search friction, asymmetric information, price impact, and funding constraints
707.2. Andrew Ang makes an important, provocative statement when he writes "Reported illiquid asset returns are not returns." He claims that people overstate the expected returns and understate the risk of illiquid assets, and he attributes this to three key biases. According to Ang, each of the following is a bias that overstates the expected returns (and/or understates the risk) of illiquid assets EXCEPT which is not accurate?
a. Survivorship bias can inflate returns by 4.0% or more
b. Infrequent sampling (aka, infrequent trading) artificially reduces risk and risk-related metrics such as volatility, correlation and beta
c. Turnover bias decreases the typical time between transactions and tends to artificially increase the expected return by 5.0% or more
d. Selection bias (aka, reporting bias) is a distortion of the sample that artificially increases (ie, overestimates) alpha and artificially decreases (ie, underestimates) beta
707.3. To adjust the infrequent trading bias introduced that is introduced into reported returns, we can "unsmooth" or "de-smooth" the reported returns. Ang suggests this is a filtering problem: "Filtering algorithms are normally used to separate signals from noise. When we’re driving on a freeway and talking on a cell phone, our phone call encounters interference—from highway overpasses and tall buildings—or the reception becomes patchy when we pass through an area without enough cell phone towers. Telecommunication engineers use clever algorithms to enhance the signal, which carries our voice, against all the static. The full transmission contains both the signal and noise, and so the true signal is less volatile than the full transmission. Thus standard filtering problems are designed to remove noise. The key difference is that unsmoothing adds noise back to the reported returns to uncover the true returns."
The essence of unsmoothing of returns is illustrated by Ang's formulas 13.1, 13.2 and 13.4 below:
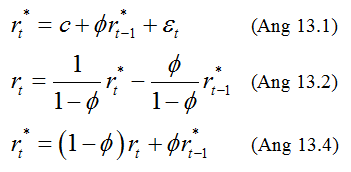
In these formulas r*(t) is the reported (aka, observed) return and r(t) is the true but unobserved return. Importantly, as is almost always the case in finance, the model used in this particular unsmoothing process makes key assumptions. However, if the assumptions are correct, then each of the following statements about the unsmoothing process is true EXCEPT which is false?
a. Unsmoothing affects only risk estimates and not expected returns
b. Unsmoothing has no effect if the observed returns are uncorrelated.
c. The true returns implied by the "transfer function" and equation 13.2, r(t), should have zero autocorrelation and generally should not be themselves forecastable
d. Due to the autocorrelation assumption, |φ| <1, the variance of the true returns will be less than the variance of the observed returns; i.e., variance[r(t)] < i.e., variance[r*(t)]
Answers here:
Last edited by a moderator:

 , I didn't realize nor quite would have expected GARP to test this yet (The Ang readings are new, usually it takes a year or so for new readings to "season"). Ang's book is really special, it is well-written, it has great sources, and it's already impacted my own thinking about investing.
, I didn't realize nor quite would have expected GARP to test this yet (The Ang readings are new, usually it takes a year or so for new readings to "season"). Ang's book is really special, it is well-written, it has great sources, and it's already impacted my own thinking about investing.