gargi.adhikari
Active Member
Hi,
In Reference to R10.P1.T1.BODIE_CH10_DIVERSIFICATION_of_RESIDUAL_RISK :-
The Weighted-Variance of the Residual Risk = Avg-Variance of Residual Risk/ N =[ (Std-Dev of Residual Risk) ^ 2 / N ] / N
The Avg-Volatility = ( Std-Dev/ N ) = 40%
So, the Last term should be just (40% ) ^2 as the 40% is the AVG-Volatility..So the AVG-Variance is just the Square of the AVG-Volatility..?
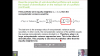

In Reference to R10.P1.T1.BODIE_CH10_DIVERSIFICATION_of_RESIDUAL_RISK :-
The Weighted-Variance of the Residual Risk = Avg-Variance of Residual Risk/ N =[ (Std-Dev of Residual Risk) ^ 2 / N ] / N
The Avg-Volatility = ( Std-Dev/ N ) = 40%
So, the Last term should be just (40% ) ^2 as the 40% is the AVG-Volatility..So the AVG-Variance is just the Square of the AVG-Volatility..?



 This looks okay to me (except there is an interim typo, the '2' does not belong in '2σ^2e(i)' above, but it does not impact the final calculation thankfully). To illustrate, let's say that n = 3 equally-weighted securities in the portfolio, where for convenience we are assuming that each security has a non-systematic volatility, σ(e_i) = 40.0% per the slide above; then the nonsystematic variance of the portfolio, σ^2(e_p) = (1/n)*Σ[σ^2(e_i)/n] = (1/n)*average_σ^2(e_i). In this example of n = 3 and σ(e_i) = 40.0%, that's two equivalent ways to get the portfolio's nonsystematic variance:
This looks okay to me (except there is an interim typo, the '2' does not belong in '2σ^2e(i)' above, but it does not impact the final calculation thankfully). To illustrate, let's say that n = 3 equally-weighted securities in the portfolio, where for convenience we are assuming that each security has a non-systematic volatility, σ(e_i) = 40.0% per the slide above; then the nonsystematic variance of the portfolio, σ^2(e_p) = (1/n)*Σ[σ^2(e_i)/n] = (1/n)*average_σ^2(e_i). In this example of n = 3 and σ(e_i) = 40.0%, that's two equivalent ways to get the portfolio's nonsystematic variance:



