gargi.adhikari
Active Member
In reference to R27.P1.T4.Hull_Ch13_15_19:Topic: WARRANT_DILUTION_HAIRCUT_FACTOR:-
The BT Notes IMO rightly sates that the Reduction/Dilution factor , the Haircut Factor = N/ ( M + N)
where M= No of Warrants ; N = No of Outstanding Shares
But The John Hull Notes state the Haircut/Reduction Factor to be = M /(M +N) ... :-(
By Hull's own deductions,
the Reduction Factor should be N / ( M+ N) .....but instead Hull states it to be as M /( M +N ) ....
Much gratitude for any clarification on this...
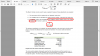
JOHN HULL NOTES:-

The BT Notes IMO rightly sates that the Reduction/Dilution factor , the Haircut Factor = N/ ( M + N)
where M= No of Warrants ; N = No of Outstanding Shares
But The John Hull Notes state the Haircut/Reduction Factor to be = M /(M +N) ... :-(
By Hull's own deductions,
the Reduction Factor should be N / ( M+ N) .....but instead Hull states it to be as M /( M +N ) ....
Much gratitude for any clarification on this...

JOHN HULL NOTES:-



