Some Quick Clarification needed on percentile VAR and Uniform VAR

[Liming]

Dear David,

It is my first time to encounter such term as "percentile and uniform distribution VAR" when doing question 20 (appended at the end) in Annotated II Power Practice. I'm used to the percentage VAR which is usually expressed with the confidence level. However, when I used this approach to calculate the answer for this question, I see that my answer has some serious discrepancy with the answer provided by you.

1) I'm having difficulty understanding how you calculated the VAR for the uniform distribution mentioned in the question. For a interval of [0,100] with equal probability of each value in between, shouldn't we assign 95% confidence level to 95 since [0,95] covers the first 95% probability? Just like what we would do with a cumulative distribution function?

2) for 20b, What exactly is the maximum expected loss from model risk at the 95th percentile? I simply multiplied 1.645 with the standard deviation for the model risk (5mm): 5*1.645 = 8.225 mm, but it seems that I have made a fundamental mistake of not being able to differentiate the percentile and percentage. How do a 95% percentile VAR differ from a 95% confidence VAR? Would we see this kind of "percentile VAR" appearing in the FRM 09 exam as I'm really thinking that this could not a "mainstream" topic?

Thanks Liming 17/11/09

Question 20:
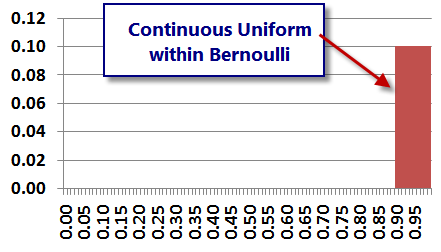
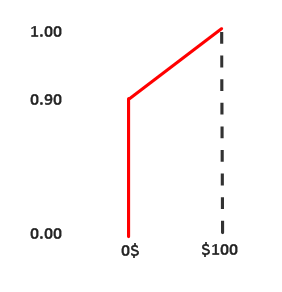
Consider the following potential operational risks. Due to a rogue trader, we estimate that over a 1 year period there is a 10% chance we could lose anywhere between € 0 and € 100MM (equal probability for all points within that range and 0 probability of any losses outside that range). Due to model risk, we estimate that over a 1 year period there is a 20% chance that we will lose € 25MM normally distributed with a standard deviation of € 5MM. Which of the following statements is true?
a. The expected loss from a rogue trader is less than the expected loss from model risk.
b. The expected loss from a rogue trader is greater than the expected loss from model risk.
c. The maximum unexpected loss from a rogue trader at the 95% confidence level is less than the maximum unexpected loss at the 95% confidence level from model risk.
d. The maximum unexpected loss at the 95% level from a rogue trader is greater than the maximum unexpected loss at the 95% level from model risk.
20b [my adds]. What exactly is the maximum expected loss from model risk at the 95th percentile?

Answer:
20. CORRECT: D. This question tests understanding of expected vs. unexpected loss. The rogue trader has an expected loss (severity multiplied by probability) of €5MM while the model risk has an expected loss of €5MM. Therefore both A and B are incorrect. We therefore must examine unexpected losses. The rogue trader has a much wider distribution (Uniform) and a lower probability of occurrence than the model risk (normal distribution). Therefore the rogue trader has a greater risk of unexpected losses.
Unexpected loss for rogue trader at 95% confidence level: 50MM - 5MM = 45MM
The loss from model risk at the 95th percentile corresponds to the 75th percentile for the normal distribution with mean 25 and standard deviation 5, so unexpected loss for model risk at 95% confidence level: < (25MM + 1.645*5MM) - 5MM < 30MM. Reference: Dowd, Chapter 16.
20b [my adds]. What exactly is the maximum expected loss from model risk at the 95th percentile? As the 5% loss tail for the entire distribution corresponds to the 25% of the normal distribution (i.e., 25% of the normal “tail” * 20% of the overall “parent” = 5%), we need the normal inverse at 75%: =NORMSINV(75%) = 0.675 0.675 * $5 MM + $25 MM mean = $28.372 So that max EL = $28.372 - $5 = $23.372 UL

 

[David Harper CFA FRM]

Hi Liming,

Can you please take a look at discussion:
http://forum.bionicturtle.com/viewthread/1401/

which includes graphic that i am copying here (for convenience):

..because I *think* your two questions are related: in both cases, you are understandably (this is a hard question!) forgetting that the loss distribution is a "child" distribution within a larger "parent" distribution.

VaR is about the loss, given then entire distribution
in the case of the rogue trader, the "parent" distribution is:" 90% of zero losses combined (piece-wise) with 10% of the uniform distribution.

similarly, in the case of model risk, piece wise:
80% of zero losses, then
20% of a normal distribution

David

 

[Maps]

Hi David,
The link is broken. Could you please reload it?

 

[David Harper CFA FRM]

Maps sorry, the thread is over four years old and I think we lost it (or cannot find it), it was a thread that referenced (I think) this 2009 P2.Operational Risk question on GARP's practice exam (Question 20): http://forum.bionicturtle.com/threads/question-20-operational-risks.3505/
... but somebody asked about this thread before and, atypically, I could not find it (b/c generally it is just a break due to our forum upgrade, but in this case, a search of the keywords does not reveal); e.g., http://forum.bionicturtle.com/threa...ds-to-75th-percentile-”-q-20.3941/#post-10367
sorry,

 

[Maps]

I understand. Thanks.

I wanted to understand this as the picture doesn't explain it to me:

1) I'm having difficulty understanding how you calculated the VAR for the uniform distribution mentioned in the question. For a interval of [0,100] with equal probability of each value in between, shouldn't we assign 95% confidence level to 95 since [0,95] covers the first 95% probability? Just like what we would do with a cumulative distribution function?

 

[David Harper CFA FRM]

Hi Maps, sure, here is the question:

20. Consider the following potential operational risks. Due to a rogue trader, we estimate that over a 1 year period there is a 10% chance we could lose anywhere between € 0 and € 100MM (equal probability for all points within that range and 0 probability of any losses outside that range). Due to model risk, we estimate that over a 1 year period there is a 20% chance that we will lose € 25MM normally distributed with a standard deviation of € 5MM. Which of the following statements is true?

We are referring to the rogue trader (not the model risk). Similar to the graphic above, the parent distribution is not a uniform distribution, rather it is a Bernoulli:

• 90% chance of zero loss, or
• 10% chance of non-zero loss determined by uniform distribution: 0 to 100 MM

In this way, we have a uniform distribution "as a child distribution within" the Bernoulli, if you will; or, piecewise distribution. The expected loss = 90%*0 + 10%*$50 = $5.0. The unexpected loss at 95% is given by the first 90% (which is all zero) plus another 5% of the parent (which is 50% of uniform), so the 95% UL = 0 + 50%*100 = $50 MM. I hope that explains, thanks,

 

[ShaktiRathore]

Hi there could i help,
According to my understanding the area under any distribution represents a cumulative probability. In this uniform distribution the probability that loss excess 95th percentile is larger as is evident from the graph as compared to normal distribution whose area(probability of loss occurring) beyond 95th percentile is much less. SO that under uniform distribution there is x% chance of loss exceeding some value Var this x % chance should be same under the normal distribution so that we need to accommodate more area under the curve which equals x% so that probably the percentile needs to go down to equal area equal to x% and thus after adjusting for this we find the normal equivalent Var for this uniform distribution.

thanks

 

[David Harper CFA FRM]

Good point ShaktiRathore ... actually, I am not sure that image correctly captures the distribution. In regard to the rogue trader, I think the cumulative distribution function (CDF) is given by this plot; i.e., until 90% the X value is zero, then a 45 degree line for the last 10%. This shows how we can retrieve the 95% UL at the midpoint between 0 and 100 (again, this is a CDF not a pdf):