GARP.FRM.PQ.P1 VAR Exceedances (garp10-p1-39)

[Priyanka_Chandak23]

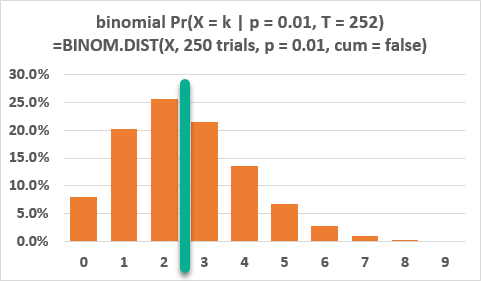
In 2006, UBS reported no exceedences on its daily 99% VaR. In 2007, UBS reported 29 exceedances. To test whether the VaR was biased, you consider using a binomial test. Assuming no serial correlation, 250 trading days, and an accurate VaR measure, you calculate the probability of observing n exceedances, for n = 0, 1, . . .

Which of the following statements is not correct?

a. At the 5% probability level, you cannot reject that the VaR was unbiased in 2006 using a binomial test.
b. The lack of exceedances in 2006 demonstrates that UBS failed to take into account the existence of fat tails in estimating the distribution of its market risk.
c. It is difficult to evaluate the implications of the lack of exceedances if the VaR is forecasted for a static portfolio and it is compared against the trading P&L.
d. At the 5% probability level, you can reject that the VaR was unbiased in 2007 using a binomial test.

Answer: b

Explanation: A and D are correct. Using 250 days in a year, the binomial test rejects for 2006 at the 8% level and for 2006 at less than the 1% level. C is correct since the trading P&L includes intra-day trading as well as market-making income. B is wrong since exceedances alone tell us nothing about the existence of fat tails.

GARP 2010
Could someone please explain point A and D correctness to me ? I am not being able to understand the binomial test here! Thanks.

 

[David Harper CFA FRM]

Hi @Priyanka_Chandak23 More discussion here (in paid area) https://forum.bionicturtle.com/threads/question-39-n-exceedances-valuation.2132
Please note below is a plot of the binomial (pmf) distribution; the probabilities actually assume 252 days not 250 as each is given by = BINOMDIST(X, 252, 0.01, false).
And I show the mean of the distribution which is 2.52 because we expected 1% * 252 days = 2.52 exceedenced per year if the VaR model is correctly calibrated.
The null hypothesis is a correct 99% VaR model

• In the case of correct (A), if we observe zero exceptions, we are in the leftmost tail, but conditional on correct model (p = 1%), there is still a 7.9% probability that random sampling variation will give us zero exceedences. In this case, for example, we can reject the null with 90% or 91% or even 92% but we cannot reject with 93% or higher confidence
• In the case of correct (D), even 6 or more exceptions will occur with less than 95% probability. So, actually, we can reject the null if we observe six (6) exceptions because 1 - binomdist(5,252,1%,true) = 1 - 95.75% = 4.25%; i.e., six or more would occur with less than 5% probability conditional on a true null. I hope that helps!

 

[Priyanka_Chandak23]

Thanks a lot, David. Appreciate your effort. In your opinion,is this one of the tricky questions of GARP or is it the regular standard based?

 

[David Harper CFA FRM]

Hi @Priyanka_Chandak23 Sure thing. In my opinion, this question is not tricky, rater it is pretty typical because it involves a real world application (backtest) of a common distribution (binomial) and further queries intuitive use of significance test. In 2016, it's a bit more typical of Part 2 where backtest is formally assigned, but it still possible under Part 1 per its Miller assignment. I hope that helps!

 

[Priyanka_Chandak23]

Thanks a lot, David.