New content added to the Study Planner this week (selected only)
Thanks to great help from @Nicole Seaman and Deepa, we are in a terrific position with respect to updating our program for the 2017 FRM syllabus. Our initial emphasis is the study notes and underlying (learning) spreadsheets. You may not be aware but I keep updated spreadsheets for almost every quantitative concept in the FRM; this allows me to be maintain rigor and fact-check practice questions. We plan to update the entire library of videos for the 2017 syllabus, also. Finally, the fresh practice question discipline will resume right after the new year. In the last week we published significant revisions to the following Study Notes
Thanks to great help from @Nicole Seaman and Deepa, we are in a terrific position with respect to updating our program for the 2017 FRM syllabus. Our initial emphasis is the study notes and underlying (learning) spreadsheets. You may not be aware but I keep updated spreadsheets for almost every quantitative concept in the FRM; this allows me to be maintain rigor and fact-check practice questions. We plan to update the entire library of videos for the 2017 syllabus, also. Finally, the fresh practice question discipline will resume right after the new year. In the last week we published significant revisions to the following Study Notes
- Diebold’s Elements of Forecasting (R15.P1.T2 Chapters 5, 6, 7 and 8). This is one of the FRM’s hardest readings. The problem--and the syllabus weakness (in my opinion, of course)--is the isolated, theoretical presentation of this time-series material. It is almost impossible to master this material without engaging in actual data and applications. As evidence, I'd point to the EOC Q&A which is basically applications. MS Excel is necessary but increasingly not sufficient. I have thoughts about how to do this. In the background I have started to gradually build R-based (best hashtag is #rstats) examples to complement our spreadsheets. Diebold uses eViews, which is a great tool. But years ago I began my own investment in learning R (https://www.r-project.org/) as my data science language of choice. And currently, it does seems like R and Python are the leading data science languages. Obviously everybody cannot become a coder or data scientist, which requires a significant and sustained commitment level. However, I do think every manager will need to become at least data-savvy and further, risk managers should aspire to be at least novice (part-time?) data scientists.
- Hull’s Chapters (R40.P2.T5) on the Risk-free rate (OIS) and Implied Volatility. Additional comments below (here).
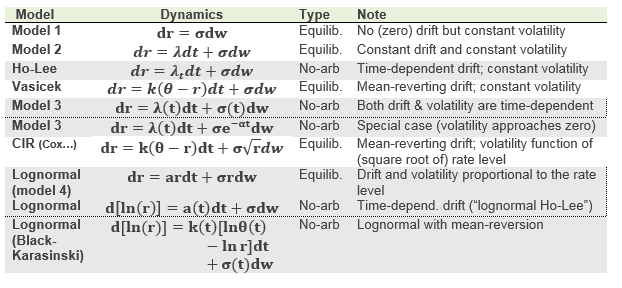
- I spent the last four or five days meticulously updating (R39.P2.T5) Tuckman’s Term Structure chapters. Additional comments below (here).
- China’s Banks Are Hiding More Than $2 Trillion in Loans http://www.wsj.com/articles/chinas-banks-are-hiding-more-than-2-trillion-in-loans-1481130392 "The surge shows how Chinese banks are trying to keep the credit spigot open to support the country’s slowing economy. Structuring financing deals as investments instead of loans frees up bank capital and makes it easier to extend loan deadlines or new credit to borrowers … If Chinese banks were required to count their investment receivables as loans, the banks would need to raise as much as $212 billion in capital, estimates UBS analyst Jason Bedford. That is not far short of the $262 billion raised by all Chinese banks in 2015.”
- BIS Quarterly Review, December 2016 https://www.bis.org/publ/qtrpdf/r_qt1612.htm
- Assessing consistency of implementation of Basel standards http://www.bis.org/bcbs/implementation/l2.htm “With today's publication of reports that assess the implementation of Basel standards in Indonesia, Japan and Singapore, the Basel Committee on Banking Supervision has completed its review of the implementation of the risk-based capital framework by all of its members.”
- Summing It Up: A Brief History of the Economy, Regulations, and Bank Data (by Federal Reserve Bank of Atlanta) https://frbatlanta.org/economy-matt...ewpoint/2016/12/06/history-of-bank-regulation
- U.S. Commission Finds Lack of ERM Is Cybersecurity Weakness http://www.garp.org/#!/risk-intelligence/technology/cyber-security/a1Z40000003NFb4EAG Report is here http://trtl.bz/2hpHOhO
- It’s Just No Fun Being a Swiss Banker Anymore (Heightened regulations, ultralow interest rates and a tech industry competing for talent have upended the profession) http://www.wsj.com/articles/the-swiss-banker-undergoes-a-tectonic-shift-1481106604
- Lloyd’s Finds Extreme Weather Can Be Accurately Modeled Independently http://www.riskmanagementmonitor.co...ther-can-be-accurately-modeled-independently/
- ClimateWise launches two reports that warn of growing protection gap due to rising impact of climate risks http://www.cisl.cam.ac.uk/business-...rn-protection-gap-due-to-impact-climate-risks
- [New Book] The Legal Risk Management Handbook: An International Guide to Protect Your Business from Legal Loss http://amzn.to/2gpS7Ai Contains this legal taxonomy:

- Glass Lewis 2017 Proxy Season Guidelines http://www.glasslewis.com/2017-proxy-season-asian-guidelines-available/ Report is here http://trtl.bz/glass-lewis-us-guidelines-2017
- Oliver Wyman Risk Journal Volume 6 http://www.oliverwyman.com/our-expertise/insights/2016/dec/oliver-wyman-risk-journal.html “Oliver Wyman today identified the top three risks facing global businesses in 2017 as it launches its 6th annual Risk Journal. The risks are: The re-emergence of nationalism and current political landscape; Technological change; and Cyberattacks” Report is here http://trtl.bz/oliver-wyman-risk-journal-no6
- Nomura Has 10 'Gray Swan' Risks That Could Roil Markets in 2017 https://www.bloomberg.com/news/arti...ey-swan-risks-that-could-roil-markets-in-2017 “7. A clearing house crisis: The systemic risks that stem from the clearing houses that were themselves introduced to contain systemic risks aren't new to regulators: financial stability watchdogs are already taking measures to deal with any potential fallouts. The interplay between struggling banks, collateral squeezes, sharp market moves in an overpriced market with central counterparties at the center could potentially lead to a crisis, in Nomura's worst-case scenario.”
- Cambridge Global Risk Outlook 2017 “CCRS identifies three important emerging trends in the global risk landscape: Emerging economies will shoulder an increasing proportion of risk-related economic loss as a result of both their accelerating economic growth and their increasing risk environment. Therefore, their risk environment is less stable; There is a growing prominence of manmade risks; A heavy contribution is expected from new or emerging risks, such as cyber attacks and infrastructure vulnerabilities.” Report is here http://trtl.bz/cambridge-global-risk-2017
- Lloyd’s City Risk Index 2015-2025 http://www.lloyds.com/cityriskindex/
- Enterprise Risk Management: Selected Agencies' Experiences Illustrate Good Practices in Managing Risk http://www.gao.gov/products/GAO-17-63 Report is here http://trtl.bz/gao-erm-dec16
- Introduction to K-means Clustering https://www.datascience.com/blog/in...tering-algorithm-learn-data-science-tutorials “K-means clustering is a type of unsupervised learning, which is used when you have unlabeled data (i.e., data without defined categories or groups). The goal of this algorithm is to find groups in the data, with the number of groups represented by the variable K. The algorithm works iteratively to assign each data point to one of K groups based on the features that are provided. Data points are clustered based on feature similarity.”
- Time is Right for LIBOR Alternative https://www.financialresearch.gov/from-the-director/2016/12/08/time-is-right-for-libor-alternative/ “The ARRC [Alternative Reference Rates Committee] has narrowed the list of potential alternatives to two: A secured repurchase agreement (repo) rate and an unsecured rate, the Overnight Bank Funding Rate. A repo is essentially a collateralized, or secured, loan when one party sells a security to another party with an agreement to repurchase it later at an agreed price. Published by the Federal Reserve Bank of New York, the Overnight Bank Funding Rate is a broad, widely accepted measure of the cost of funds for U.S. banks based on the federal funds rate and those on overnight Eurodollar deposits.”
- The Man Who Invented the World’s Most Important Number (LIBOR) https://www.bloomberg.com/news/features/2016-11-29/the-man-who-invented-libor-iw3fpmed
- What’s up with the term premium? https://ftalphaville.ft.com/2016/12/01/2180569/whats-up-with-the-term-premium/
- Why Are Long-Term Interest Rates So Low? http://www.frbsf.org/economic-resea...mber/why-are-long-term-interest-rates-so-low/ “To understand why rates are low, it is useful to consider the two key components of long-term interest rates. The first is the average of expected future short-term interest rates—the expectations component. The second component is the term premium, which includes compensation to investors for the risk of holding long-term bonds but is also a catch-all for other factors beyond the expectations component that affect long-term rates.”
- About the challenges of sovereign risk modelling https://www.linkedin.com/pulse/challenges-sovereign-risk-modelling-bernhard-obenhuber
- Types of Financial Models (Top 4 in Investment Banking) http://www.wallstreetmojo.com/types-of-financial-models
- Top Security Threats to Companies in 2017 https://www.pinkerton.com/blog/top-company-security-threats-2017/ “Top Security Threat #1: Lone Wolf Attacks and Corporate Travel … Top Security Threat #2: Natural Disasters Packing More Punch”
- Is Private Company Ownership a Risk for Mutual Funds? http://news.morningstar.com/articlenet/article.aspx?id=783216 “This example highlights a risk of private-company ownership in an open-end structure. Investors can be fickle and may not stick around when the fund is going through a rough spell. Managers can be forced to trim or sell publicly traded stocks they may have preferred to keep. Portfolio construction can also appear out of whack, as the private, illiquid holdings soak up more of a fund's assets and drive more of the fund's performance than perhaps was initially intended.”
- A Dallas public pension fund suffers a run http://www.economist.com/news/finan...en-brewing-decades-and-it-not-confined-dallas “BANK runs, with depositors queuing round the block to get their cash, are a familiar occurrence in history. A run on a pension fund is virtually unprecedented. But that is what is happening in Dallas, where policemen and firefighters are pulling money out of their city’s chronically underfunded plan, and Mike Rawlings, the mayor, is suing to stop them … The crisis is the result of three linked issues: overgenerous pension promises; the flawed nature of public-sector pension accounting in America; and some bad investment decisions. In order to pay the generous benefits, the scheme counted on an investment return of 8.5% a year, absurdly high in a world where the yield on ten-year Treasury bonds has been hovering in a range of 1.5-3%. So the scheme opted for riskier assets in private equity and property. But the strategy did not work; the value of its investments declined by $263m in 2014 and $396m in 2015, thanks largely to write-downs of those risky assets.”
- South Carolina's looming pension crisis http://trtl.bz/2gB5Bwh
Last edited by a moderator:







 . Finally, there are two flavors of lognormal model. I hope that is helpful!
. Finally, there are two flavors of lognormal model. I hope that is helpful!