Question: The BSM formula is actually simple except for N(d1) and N(d2) in the case of the call, and N(-d1) and N(-d2) in the case of the put. Will the exam always provide N(d1) and N(d2) or do we need to know how to calculate them?
Answer: That's a good point that BSM is simple except for the standard normal cumulative distribution functions; aka, normal CDFs. After all, the minimum value of the call on a non-dividend paying is given by min[call] = S(0) - K*exp(-rT) which can be understood intuitively. The minimum value is the option's value if the volatility is zero, so we can imagine the addition of the N(.) functions as increasing the option's value to account for non-zero volatility. It is helpful to have a bit of an intuitive understanding of why N(d2) is the probability that a call option will expire in the money (ie, will be exercised) in the risk-neutral world; see http://trtl.bz/merton-model-summary. While it is more difficult to get an intuition of N(d1), at least memorize that N(d1) is the Greek percentage delta of a non-dividend paying stock, and please don't forget that for a dividend-paying stock call option delta is given by exp(-qT)*N(d1). With that context, let's finally answer the question...
As of 2017, authorized exam calculators include the Texas Instruments (TI) BA II Plus and Hewlett Packard (HP) 12C which do not naturally return CDFs. Therefore, you cannot be expected to retrieve N(d1) or N(d2) from scratch. The most likely scenario is that these probability values will be provided as assumptions. For example, here is a snippet from GARP's 2015 Part 1 Practice Exam, Question 11:

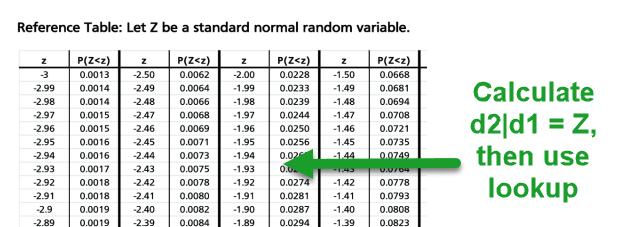
Another possible scenario is for the question to require you to calculate d2 or d1 and then retrieve N(d2) or N(d1) by using a provided Z-lookup table. For example, here is the provided Z lookup table in GARP's 2017 Part 2 Practice Exam:
A final possibility--although this seems unlikely--is for the (d2) or (d1) value to conveniently calculate to a recognizable quantile such as -2.33, -1.65, +1.65, +2.33 or even +/- 1.96 because if d2 is conveniently equal to 1.65 then we do not need a calculator to realize that N(1.65) equals about 95.0%.
Finally, please remember that d2 = d1 - σ*sqrt(T). Thanks!
Answer: That's a good point that BSM is simple except for the standard normal cumulative distribution functions; aka, normal CDFs. After all, the minimum value of the call on a non-dividend paying is given by min[call] = S(0) - K*exp(-rT) which can be understood intuitively. The minimum value is the option's value if the volatility is zero, so we can imagine the addition of the N(.) functions as increasing the option's value to account for non-zero volatility. It is helpful to have a bit of an intuitive understanding of why N(d2) is the probability that a call option will expire in the money (ie, will be exercised) in the risk-neutral world; see http://trtl.bz/merton-model-summary. While it is more difficult to get an intuition of N(d1), at least memorize that N(d1) is the Greek percentage delta of a non-dividend paying stock, and please don't forget that for a dividend-paying stock call option delta is given by exp(-qT)*N(d1). With that context, let's finally answer the question...
As of 2017, authorized exam calculators include the Texas Instruments (TI) BA II Plus and Hewlett Packard (HP) 12C which do not naturally return CDFs. Therefore, you cannot be expected to retrieve N(d1) or N(d2) from scratch. The most likely scenario is that these probability values will be provided as assumptions. For example, here is a snippet from GARP's 2015 Part 1 Practice Exam, Question 11:

Another possible scenario is for the question to require you to calculate d2 or d1 and then retrieve N(d2) or N(d1) by using a provided Z-lookup table. For example, here is the provided Z lookup table in GARP's 2017 Part 2 Practice Exam:

A final possibility--although this seems unlikely--is for the (d2) or (d1) value to conveniently calculate to a recognizable quantile such as -2.33, -1.65, +1.65, +2.33 or even +/- 1.96 because if d2 is conveniently equal to 1.65 then we do not need a calculator to realize that N(1.65) equals about 95.0%.
Finally, please remember that d2 = d1 - σ*sqrt(T). Thanks!
