Hello,
I have just started with the first instructional video of part 2, covering market risk measures.
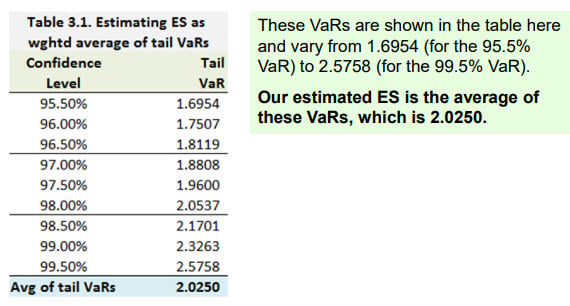
In the ES calculation, I do understand the concept, but what is confusing me after many hours of trying to figure it out, is the calculation of the tail VaRs. For example, for the 99% CL, the z-score of the normal distribution is (1.99/2)= 0.995. Using the z-score table, the normal deviate should be 2.575. Given that the mean is zero and the standard deviation is 1, normal VaR is -0 + 1*2.575 = 2.575. However, the corresponding tail VaR in the example is 2.3263.
The same applies for the normal deviate calculations, at different confidence levels, in the example of the estimation of exponential spectral risk measures as weighted average of VaRs. The corresponding normal deviates for each CL are nowhere near the true values. Please help, what can I be doing wrong?
Thanks.
I have just started with the first instructional video of part 2, covering market risk measures.
In the ES calculation, I do understand the concept, but what is confusing me after many hours of trying to figure it out, is the calculation of the tail VaRs. For example, for the 99% CL, the z-score of the normal distribution is (1.99/2)= 0.995. Using the z-score table, the normal deviate should be 2.575. Given that the mean is zero and the standard deviation is 1, normal VaR is -0 + 1*2.575 = 2.575. However, the corresponding tail VaR in the example is 2.3263.
The same applies for the normal deviate calculations, at different confidence levels, in the example of the estimation of exponential spectral risk measures as weighted average of VaRs. The corresponding normal deviates for each CL are nowhere near the true values. Please help, what can I be doing wrong?
Thanks.