Hi, I could not find a easy way to solve this question for Interest rates using bootstrap? can someone please help me?
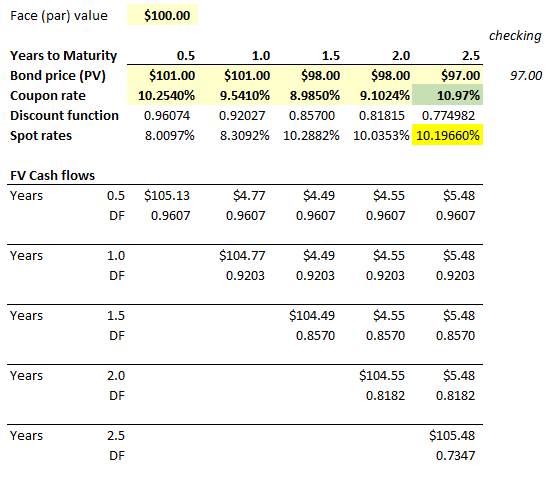
Find coupon rate for 2nd year (X in below table)
time -0.5- 1- 1.5- 2
Bond price 99- 98- 97- 95
Coupon rate 2.0000%- 3.0000%- 3.5000%- X.0000%
Spot rate 4.0001%- 5.0208%- 5.5514%- 7.6993%
Find coupon rate for 2nd year (X in below table)
time -0.5- 1- 1.5- 2
Bond price 99- 98- 97- 95
Coupon rate 2.0000%- 3.0000%- 3.5000%- X.0000%
Spot rate 4.0001%- 5.0208%- 5.5514%- 7.6993%