Kendall Tau (example)

[equanimity]

I'm interested in solving for Kendall Tau. Can someone help me with this?

The rankings for some stock returns are:

X Rank..... Y Rank
1.................... 2
2.................... 4
3.................... 1
4.................... 3
5.................... 5

Thanks!

 

[David Harper CFA FRM]

Hi @equanimity You can use my XLS https://www.dropbox.com/s/rxk6s6cvd08mb5n/MR-9-kendalls-tau.xlsx?dl=0 which is from my note here at https://forum.bionicturtle.com/thre...lls-tau-and-concordant-discordant-pairs.8209/

Let me know if you have any questions, once you practice a few, it becomes possible to visualize; I created a graphic her for visualizing concordant/discordant pairs https://forum.bionicturtle.com/threads/week-in-risk-april-4th.9463/#post-41467 which is also below

 

[equanimity]

Thank you, David.

Yes, I see 7 concordant pairs and 3 discordant pairs. Given the following:

(C - D) / (C + D)

4 / 10 --> 0.4

Thanks again.

 

[[email protected]]

@ @David Harper CFA FRM CIPM Thanks David . the example was really helpful.

Hopefully we will get question on kendall tomorrow

 

[Arnaudc]

Thanks a lot @David Harper CFA FRM , I had no clue how to calculate this before reading your excel...

 

[Ali Ehsan Abbas]

Thanks a bunch @David Harper CFA FRM...but please bear with me...i am not able to follow through...

Please provide an alternate view...maybe with examples:

(1,3)(3,1)?
(1,4)(2,3)?
(2,4)(3,3)?

Also, if we look at earlier definition on "neither" where xt=xt* or yt=yt*...say (1,4)(2,4) as in your example...wouldn't that create a "double 4"...my intuition says "4" must be unique to one pair and one pair only?

Thanks a lot

 

[FrmL2_Aspirant]

I think, a neither case would be 1,3 and 1,4 which is technically not possible, however, David can explain best..

thanks,
Smita

 

[David Harper CFA FRM]

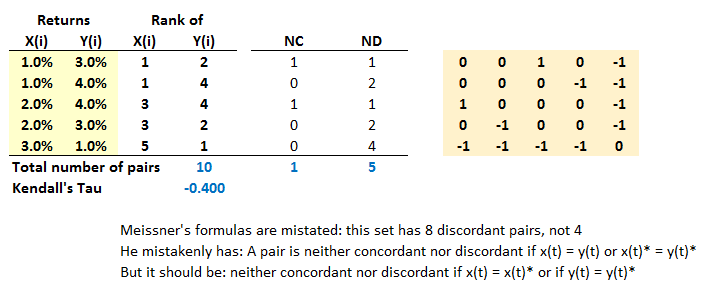
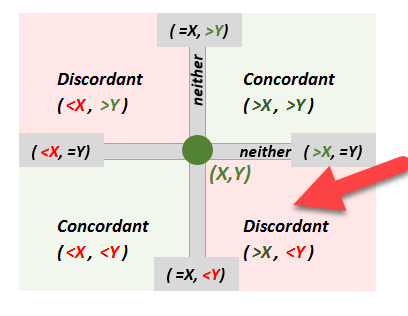
@Ali Ehsan Abbas I just inserted two columns, for returns of X(i) and Y(i), before the rankings, so the rankings are now calculated based on the (yellow cells) input returns. I included your (1,3), (1,4), (2,4), (3,1) and (2,3) ... although oops these are the returns not the ranks ... no matter, I think you will get the point. Here is the XLS in case you want to experiment: https://www.dropbox.com/s/95ye8eav6x5udvq/0514-MR-9-kendalls-tau.xlsx?dl=0

So, please notice, with respect to "must each rank be unique," I think it depends on how the rankings are defined. I simply duplicated returns and used Excel's =RANK.EQ() function such that, you can see below, the rank of both X(i) and Y(i) includes a duplicate. In fact, X(i) includes two duplicates because the ranking is given by {1, 1, 3, 3, 5}. You will notice this is returning a kendall's tau of -0.40 based on fully 10 - 1 NC - 5 ND = 4 pairs which are neither. For example, one of these "neither" pairs is {1,2}, {1,4} because x(t)=x(t)* Here are two examples from this set:

• In terms of ranks (not % returns), the pairs (1,2),(3,4) are concordant because 1<3 and 2<4
• but the pairs (1,2),(5,1) are discordant because 1<5 but 2>1

Separately in terms of your sets:

• (1,3)(3,1) as (x,y), (x*,y*): x<x* but y>y* or 1<3 but 3>1 so this is discordant
• (1,4)(2,3): 1<2 but 4>3 so this is also discordant
• (2,4)(3,3): 2<3 but 4>3 so this is also discordant. In all three cases, as we compare X(i), the second pairs has a greater X(i) value but the Y(i) goes in the other direction such that the second Y(i) has a lesser value

My graphic is merely meant to enable a visualization (but maybe it's not helpful to everybody). Consider taking your pairs and translating the second pairs so that it is expressed in relative terms:

• (1,3),(3,1) --> (1,3),(+2, -2)
• (1,4),(2,3) --> (1,4),(+1, -1)
• (2,4), (3,3) --> (2,4),(+1, -1) ... see how this easily identifies discordant. And just to add a "neither" to the mix:
• (2,4),(3,4) --> (2,4),(+1,0) ... and the zero confirms neither. So that's all that i meant by my quandrants! In the case of your three examples, in relative terms, the second pairs are all in the same quadrant (see below). I hope that's helpful!

 

[Ali Ehsan Abbas]

Very helpful @David Harper CFA FRM

Strange how other sources employ approach resulting in significantly different results.

From what i was able to read so far this is my synopsis viz. the above workout:

(1,3)(3,1): Discordant cuz 1<3 BUT 3>1
(1,4)(2,3): Concordant cuz 1<4 AND 2<3
(2,4)(4,3): Discordant cuz 2<4 BUT 4>3
Any pair including (X,Y) where X=Y (as opposed to X=Xt is neither.

Thinking about it, it seems like we are consistently comparing Xs to Xs and Ys to Ys so your approach makes it consistent.

I've bogged you with this...a line or two of your view is highly appreciated.

 

[David Harper CFA FRM]

Hi @Ali Ehsan Abbas you haven't bogged me, it's how i learn too ... but I am not comparing X to Y. In the pair (X1, Y1), (X2,Y2) we compare X1 to X2 and then we compare Y1 to Y2, so with respect to your second pair (1,4)(2,3), I would say that is discordant because 1<2 BUT 4>3. The "neither" happens when either X1 = X2 or Y1 = Y2. As mentioned above, one of the pairs in my screenshot, {1,2}, {1,4}, is NEITHER because 1 = 1 and 2 < 4. I hope that's helpful!