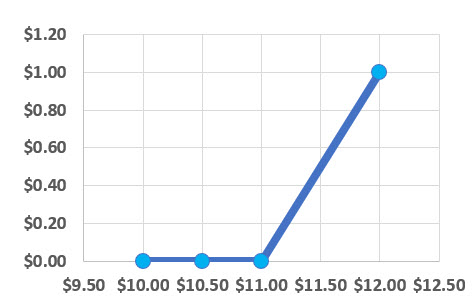
Hi all, can anyone tell me the following:
stock price is $10
1 hour before expiry.
In that hour it is expected that there are the following possibilities:
-10% chance that the stock moves 10%
-20% chance the stock moves with 20%
-30% chance the stock moves with 5%
-40% chance the stock stays where it is.
from this information, can I calculate N(d1) and N(d1) for strike 11?
stock price is $10
1 hour before expiry.
In that hour it is expected that there are the following possibilities:
-10% chance that the stock moves 10%
-20% chance the stock moves with 20%
-30% chance the stock moves with 5%
-40% chance the stock stays where it is.
from this information, can I calculate N(d1) and N(d1) for strike 11?

 But I have technical issues to varying degrees with all of these solutions ...
But I have technical issues to varying degrees with all of these solutions ...