Learning objectives: Apply the concept of marginal VaR to guide decisions about portfolio VaR. Explain the risk-minimizing position and the risk and return-optimizing position of a portfolio. Explain the difference between risk management and portfolio management and describe how to use marginal VaR in portfolio management.
Questions:
21.6.1. Emily manages a $20.0 million portfolio allocated into two positions (aka, two components): a Technology ETF, and a Real Estate Investment Trust (REIT) ETF. She compares four different allocations, where the weight assigned to the Tech ETF component is either 35.0%, 50.0%, 65%, or 80.0%.
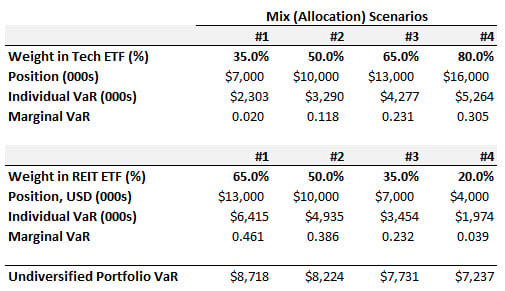
If her goal is to minimize the portfolio's diversified value at risk (VaR), which of the above allocations is best?
a. Mix #1 with 35.0% allocated to the Tech ETF
b. Mix #2 with 50.0% allocated to the Tech ETF
c. Mix #3 with 65.0% allocated to the Tech ETF
d. Mix #4 with 80.0% allocated to the Tech ETF
21.6.2. Peter manages a $10.0 million portfolio allocated into two positions (aka, two components): an Energy ETF, and a Healthcare ETF. He compares four different allocations, where the weight assigned to the Energy ETF component is either 45.0%, 60.0%, 75%, or 90.0%. The Energy ETF offers an expected excess (i.e., in excess of the riskfree rate) of 6.0% while the Healthcare ETF offers an excess return of 12.0%.
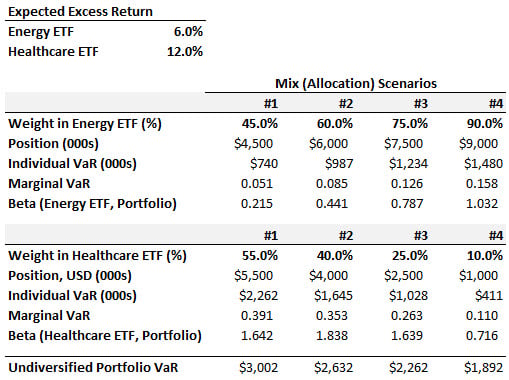
Peter's goal is not risk minimization, but rather to maximize the ratio of expected excess return to risk. Put another way, he seeks the most efficient portfolio. Given his goal, which of the above allocations is best?
a. Mix #1 with 45.0% allocated to the Energy ETF
b. Mix #2 with 60.0% allocated to the Energy ETF
c. Mix #3 with 75.0% allocated to the Energy ETF
d. Mix #4 with 90.0% allocated to the Energy ETF
21.6.3. Consider a $30.0 million portfolio with two positions:
a. The Incremental VaR of the Materials ETF position is larger than the Incremental VaR of the Consumer position
b. Each position's Component VaR is less than its Incremental VaR
c. If the correlation doubles to +0.30 then each position's Component VaR will increase
d. To either decrease the portfolio's risk (aka, portfolio VaR) or increase the portfolio's Sharpe ratio, we should reallocate from the Materials ETF to the Consumer ETF; i.e., reduce Materials position and increase the Consumer position
Answers here:
Questions:
21.6.1. Emily manages a $20.0 million portfolio allocated into two positions (aka, two components): a Technology ETF, and a Real Estate Investment Trust (REIT) ETF. She compares four different allocations, where the weight assigned to the Tech ETF component is either 35.0%, 50.0%, 65%, or 80.0%.

If her goal is to minimize the portfolio's diversified value at risk (VaR), which of the above allocations is best?
a. Mix #1 with 35.0% allocated to the Tech ETF
b. Mix #2 with 50.0% allocated to the Tech ETF
c. Mix #3 with 65.0% allocated to the Tech ETF
d. Mix #4 with 80.0% allocated to the Tech ETF
21.6.2. Peter manages a $10.0 million portfolio allocated into two positions (aka, two components): an Energy ETF, and a Healthcare ETF. He compares four different allocations, where the weight assigned to the Energy ETF component is either 45.0%, 60.0%, 75%, or 90.0%. The Energy ETF offers an expected excess (i.e., in excess of the riskfree rate) of 6.0% while the Healthcare ETF offers an excess return of 12.0%.

Peter's goal is not risk minimization, but rather to maximize the ratio of expected excess return to risk. Put another way, he seeks the most efficient portfolio. Given his goal, which of the above allocations is best?
a. Mix #1 with 45.0% allocated to the Energy ETF
b. Mix #2 with 60.0% allocated to the Energy ETF
c. Mix #3 with 75.0% allocated to the Energy ETF
d. Mix #4 with 90.0% allocated to the Energy ETF
21.6.3. Consider a $30.0 million portfolio with two positions:
- $20.0 million position in a Consumer ETF with expected excess return of 4.0%, volatility of 12.0%, and marginal VaR (ΔVaR) equal to 0.122
- $10.0 million position in a Materials ETF with expected excess return of 8.0%, volatility of 38.0%, and marginal VaR (ΔVaR) equal to 0.543
- The correlation between the two positions is +0.150
a. The Incremental VaR of the Materials ETF position is larger than the Incremental VaR of the Consumer position
b. Each position's Component VaR is less than its Incremental VaR
c. If the correlation doubles to +0.30 then each position's Component VaR will increase
d. To either decrease the portfolio's risk (aka, portfolio VaR) or increase the portfolio's Sharpe ratio, we should reallocate from the Materials ETF to the Consumer ETF; i.e., reduce Materials position and increase the Consumer position
Answers here:
Last edited by a moderator:
