VAR using POT
- Thread starter rickm123
- Start date
Hi Rick, It's not a typo but rather following Dowd: where n = number of loss observations and N(u) is the number of [far fewer] observations in the extreme tail, for example, Dowd has N(u)/n = 4% (displayed in calcs) but the formula has n/N(u)--but 25 = 1/4% is not as intuitive--so the calculation performs: 1/4% = 1/(N(u)/n) = n/N(u) per the formula.
In other words, I can only assume the 4% extreme threshold is used, because it is the more intuitive way to express the threshold, but the formula then uses 1/4%, so does use n/N(u) = 25
(the VaR POT formula is NOT, imo, directly intuitive, in parts due to the units confusion. It is really only understood as a solution to the parent CDF.) I hope that helps,
In other words, I can only assume the 4% extreme threshold is used, because it is the more intuitive way to express the threshold, but the formula then uses 1/4%, so does use n/N(u) = 25
(the VaR POT formula is NOT, imo, directly intuitive, in parts due to the units confusion. It is really only understood as a solution to the parent CDF.) I hope that helps,
irwinchung
Member
Hi David,
So Dowd is using a 2% exceedence and 4% quantile to calculate the 99.5% VAR?
So let's say there are 100 observations, he picks 2% loss as a threshold, he sees that 4 observations exceed the threshold (4%) or N(u)/n
His boss say hey what is the 99.5 %var? The worst (1) observation is say 3% loss but that is only 99% var ( and that itself is a crude empirical method)
He can assume normality, get mean, variance, and the 99.5 var that way but he decides to use EVT
So he plugs in the VAR formula (based on GP dist) and gets 3.95%
So 2% and 4% are essentially just "anchors" then? he could have selected 3% and 1% if he wanted to?
Can you confirm if I am understanding this right?
Thanks very much.
So Dowd is using a 2% exceedence and 4% quantile to calculate the 99.5% VAR?
So let's say there are 100 observations, he picks 2% loss as a threshold, he sees that 4 observations exceed the threshold (4%) or N(u)/n
His boss say hey what is the 99.5 %var? The worst (1) observation is say 3% loss but that is only 99% var ( and that itself is a crude empirical method)
He can assume normality, get mean, variance, and the 99.5 var that way but he decides to use EVT
So he plugs in the VAR formula (based on GP dist) and gets 3.95%
So 2% and 4% are essentially just "anchors" then? he could have selected 3% and 1% if he wanted to?
Can you confirm if I am understanding this right?
Thanks very much.
Hi @irwinchung Sorry I didn't get to your query sooner, I've been today catching up on some threads that I missed. Regarding your question, yes I think you are partially correct; the theshold is a selectable (movable) anchor (in your example, the 2%). However, the percentage of exceedences ought to be largely informed the data (given the selected threshold). See the screenshot below, it is from this XLS at https://www.dropbox.com/s/nkum6b971naxxn1/0524-garp17-p2-1-evt.xlsx?dl=0 (in case you are interested, I have been reviewing GARP's revised 2017 practice question and it happens to be that the first question is about POT GPD, see my note here at https://forum.bionicturtle.com/thre...iew-of-garps-2017-part-2-practice-exam.10510/ ). In any case ...
At the very bottom (below) I created a set of artificial tail data (losses in positive; e.g., the worst loss over 100 days was -3.9%, the second worst loss was -3.10%). In the first column, I decide the threshold, u, is 1.50% (third row input), which is a selectable "anchor" to your point. Given the data, that implies N(u)/N = 6/100 = 6.0%. (All of these distributions have the same scale and tail index, btw, the same Dowd assumes; changing them impact the POT GPD ES but do not impact the VaR). And just to illustrate, the 94.0% VaR here is the 1.50 threshold, as we should expect. In the next column, I simply ask for the 95.0% VaR and 95.0% ES, which are both above the 1.50 threshold (as we should expect). Then in the third to fifth column, given the same data set, I simply increased the POT threshold from 1.50% to 2.0%; but this implies that N(u)/N reduces from 6.0% to 4/100 or 4.0%. The EVT ES is reacting to this "shifting of the threshold anchor." In the final three columns, as you suggest, I shift the threshold (again) to 3.0%; although, just to experiment, the very final column alters the underlying dataset so that only 1% of observations are "above" (i..e., worse than) the 3.0% threshold. I think the reactions, if we think about it, are all as expected. I hope that's helpful and I hope the exam went well? Thanks!
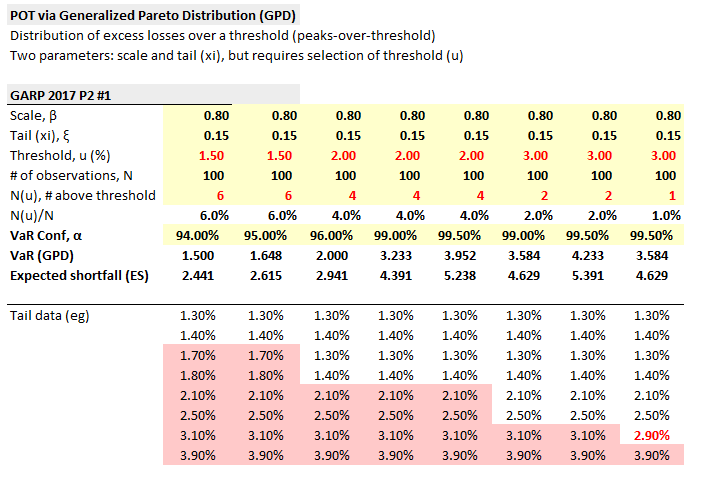
At the very bottom (below) I created a set of artificial tail data (losses in positive; e.g., the worst loss over 100 days was -3.9%, the second worst loss was -3.10%). In the first column, I decide the threshold, u, is 1.50% (third row input), which is a selectable "anchor" to your point. Given the data, that implies N(u)/N = 6/100 = 6.0%. (All of these distributions have the same scale and tail index, btw, the same Dowd assumes; changing them impact the POT GPD ES but do not impact the VaR). And just to illustrate, the 94.0% VaR here is the 1.50 threshold, as we should expect. In the next column, I simply ask for the 95.0% VaR and 95.0% ES, which are both above the 1.50 threshold (as we should expect). Then in the third to fifth column, given the same data set, I simply increased the POT threshold from 1.50% to 2.0%; but this implies that N(u)/N reduces from 6.0% to 4/100 or 4.0%. The EVT ES is reacting to this "shifting of the threshold anchor." In the final three columns, as you suggest, I shift the threshold (again) to 3.0%; although, just to experiment, the very final column alters the underlying dataset so that only 1% of observations are "above" (i..e., worse than) the 3.0% threshold. I think the reactions, if we think about it, are all as expected. I hope that's helpful and I hope the exam went well? Thanks!
Similar threads
